Calculate Kepler’s equation by iterative calculation method using Go

Background

To learn the Go language and space engineering, let’s solve Kepler’s equation using the iterative method (Newton-Raphson method).

Kepler’s equation

Kepler’s equation is an equation expressed as follows. (the eccentric anomaly (E), mean anomaly (M), and eccentricity (e))

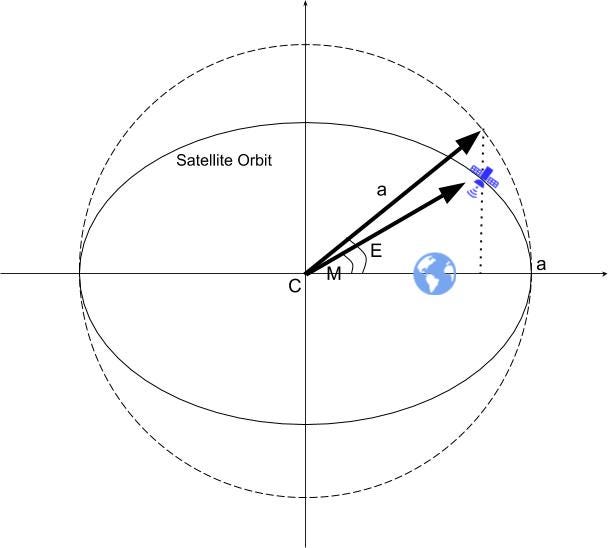
When considering an elliptical orbit of a satellite with Earth as its focus, M and E can be represented in the following diagram, where “a” is the semi-major axis.

This equation cannot be solved by ordinary calculations and requires iterative methods like the Newton-Raphson method.

Defining the equation as eq1 below and rewriting it as eq2 below allows for iterative calculations. (The detailed derivation method is skipped.)

eq1

eq2

Implement with Go

Now, let’s implement this in Go.

First, set the constants:

// Earth's gravitational constant
const gravitationalConstant = 398600.4

And create a function named MeanAnomaly to calculate the mean anomaly (M):

func MeanAnomaly(a, deltaT float64)float64{
    return math.Sqrt(gravitationalConstant/math.Pow(a, 3)) * deltaT
}

“a” represents the semi-major axis (km), and “deltaT” is the elapsed time (seconds) from the epoch to the desired moment. This function returns the mean anomaly (radians).

Define Kepler’s equation as a closure:

func KeplerEquation(e, M float64) func(Ebefore float64) float64{
    return func(Ebefore float64)float64{
        FE := Ebefore - e*math.Sin(Ebefore) - M
        Eafter := Ebefore - FE/(1-e*math.Cos(Ebefore))
        return Eafter
    }
}

The arguments represent the following:

• e: eccentricity
• M: mean anomaly
• Ebefore: n-th eccentric anomaly
• Eafter: (n+1)-th eccentric anomaly

By inputting these arguments, you can execute the return function repeatedly.

Now, implement a function to calculate the closure of Kepler’s equation using the Newton-Raphson method:

func NewtonRaphson(e, before, ae float64) float64 {
    equation := KeplerEquation(e, before)
    var after float64
    err := 100.0 // Initialize error (if 0, the loop won't run)
    count := 0
    for ; err > ae; {
        after = equation(before)
        err = math.Abs(after - before)
        fmt.Println("Error: ", err)
        before = after
        count = count + 1
        fmt.Println("Iteration:", count, "times")
        fmt.Println("----")
    }
    return after
}

Specify the allowable error (ae) as an argument. When the calculation error becomes smaller than the allowable error, break the for loop and return the calculation result.

Now, define the main function and use it to confirm that the correct calculation result is obtained. Calculate with the semi-major axis "a" as 2000 km, elapsed time "deltaT" as 3600 seconds, eccentricity "e" as 0.75, and allowable error as 0.0001.

func main() {
    fmt.Println("Calculating the eccentric anomaly E using Kepler's equation:")
    M := MeanAnomaly(2000, 3600)
    Mdigree := int(M * 180 / math.Pi) % 360
    E := NewtonRaphson(0.75, M, 0.0001)
    Edigree := int(E * 180 / math.Pi) % 360
 
    Mrad := math.Round(M*100)/100
    Erad := math.Round(E*100)/100
    fmt.Printf("\nMean anomaly M is %vrad, %v°.", Mrad, Mdigree)
    fmt.Printf("\nEccentric anomaly E is %vrad, %v°.", Erad, Edigree)
}

The output results will be as follows:

Calculating the eccentric anomaly E using Kepler's equation:
Error:  0.7393437287609679
Iteration: 1 times
----
Error:  0.1667982273838291
Iteration: 2 times
----
Error:  0.016917352484746573
Iteration: 3 times
----
Error:  0.00016185780524580196
Iteration: 4 times
----
Error:  1.4669140568912553e-08
Iteration: 5 times
----
Mean anomaly M is 25.41rad, 15°.
Eccentric anomaly E is 25.97rad, 47°.

Conclusion

Comparing the calculation results with those from the following website (in Japanese) shows that, although there is a slight calculation error, the results are almost correct.

https://keisan.casio.jp/exec/user/1251722629

Complete code

Here is the complete code for reference:

package main
import (
    "fmt"
    "math"
)
// Earth's gravitational constant
const gravitationalConstant = 398600.4
// Mean anomaly
func MeanAnomaly(a, deltaT float64)float64{
    return math.Sqrt(gravitationalConstant/math.Pow(a, 3)) * deltaT
}
// Kepler's equation
func KeplerEquation(e, M float64) func(Ebefore float64) float64{
    return func(Ebefore float64)float64{
        FE := Ebefore - e*math.Sin(Ebefore) - M
        Eafter := Ebefore - FE/(1-e*math.Cos(Ebefore))
        return Eafter
    }
}
// Solving Kepler's equation with Newton-Raphson method
func NewtonRaphson(e, before, a float64) float64 {
    equation := KeplerEquation(e, before)
    var after float64
    err := 100.0 // Initialize error (if 0, the loop won't run)
    count := 0
    for ; err > a; {
        after = equation(before)
        err = math.Abs(after - before)
        fmt.Println("Error: ", err)
        before = after
        count = count + 1
        fmt.Println("Iteration:", count, "times")
        fmt.Println("----")
    }
    return after
}

func main() {
    fmt.Println("Calculating the eccentric anomaly E using Kepler's equation:")
    M := MeanAnomaly(2000, 3600)
    Mdigree := int(M * 180 / math.Pi) % 360
    E := NewtonRaphson(0.75, M, 0.0001)
    Edigree := int(E * 180 / math.Pi) % 360
 
    Mrad := math.Round(M*100)/100
    Erad := math.Round(E*100)/100
    fmt.Printf("\nMean anomaly M is %vrad, %v°.", Mrad, Mdigree)
    fmt.Printf("\nEccentric anomaly E is %vrad, %v°.", Erad, Edigree)
}